Contenu

Jusqu’à maintenant, tous les objets que nous avons insérés dans nos fichiers se plaçaient par défaut au centre de notre scène, au point 0 0 0.

Nous allons donc apprendre à déplacer les objets dans l’espace; ce qu’on appelle une translation. Pour cela, nous appliquons une transformation à l’objet, à l’aide d’un bloc de code Transform { … }, qui entoure les blocs de code habituel.

Transform { translation x y z children [ … description d’un objet … ] }

Notez le terme children [ ... ] qui indique au programme que la transformation doit s’effectuer sur tous les objets compris entre les deux crochets.

• Regardez l’exemple suivant (translation.wrl) qui déplace un cube rouge à droite d’un cube bleu:

  #VRML V2.0 utf8 #Un cube bleu au côté d’un cube rouge #Description d’un cube bleu Shape { geometry Box { size 2 2 2 } appearance Appearance { material Material { diffuseColor 0 0 1 } } } #Déplacement d’un cube rouge Transform { translation 2 0 0 children [ Shape { geometry Box { size 2 2 2 } appearance Appearance { material Material { diffuseColor 1 0 0 } } } ] }

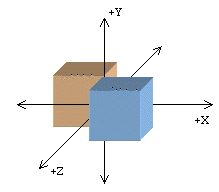
  Dans cet exemple, le cube rouge est déplacé sur l’axe de la largeur X, mais il ne bouge ni en Y ni en Z. La translation était de 2 en X, 0 en Y et 0 en Z. Cela signifie aussi que le centre du cube se trouvait sur le point 2 0 0.

• Modifiez le fichier pour effectuer une translation de -2 en X, 0 en Y et -2 en Z.

  Avant de regarder le fichier dans Firefox, essayez de l’imaginer et de déterminer où sera placé le cube rouge. (translation2.wrl)

Exercice: Quelle est la translation à effectuer pour que les axes XYZ se trouvent à l'intersection des deux cubes? (dans un ficher nommé "translation3.wrl")

Exemple graphique:

• Afin de vérifier où se trouvent les objets par rapport aux axes XYZ, vous pouvez insérer le code suivant qui fera appel au fichier axes.wrl juste après la ligne #VRML V2.0 utf8:

  #Importe les axes XYZ Inline { url "http://www.ecole-moser.ch/atelier_vrml/axes.wrl" bboxSize 20 20 20 bboxCenter 0 0 0 }

• Sans vous révéler les valeurs des deux translations qui sont remplacées par des ?, voici à quoi doit ressembler le code dans votre nouveau fichier:

  #VRML V2.0 utf8 #Un cube bleu au côté d’un cube rouge #Importe les axes XYZ Inline { url "http://www.ecole-moser.ch/atelier_vrml/axes.wrl" bboxSize 20 20 20 bboxCenter 0 0 0 } #Description et déplacement d’un cube bleu Transform { translation ? ? ? children [ Shape { geometry Box { size 2 2 2 } appearance Appearance { material Material { diffuseColor 0 0 1 } } } ] } #Description et déplacement d’un cube rouge Transform { translation ? ? ? children [ Shape { geometry Box { size 2 2 2 } appearance Appearance { material Material { diffuseColor 1 0 0 } } } ] }

Jusqu’à maintenant, tous les cônes et les cylindres que nous sommes capables de décrire sont pointés vers le haut. Nous nous rendons compte de la nécessité de savoir faire pivoter un objet sur lui-même, ce qu’on nomme en VRML la rotation.

La rotation est une transformation que l’on effectue de la même manière que la translation, à l’aide d’un bloc de code Transform { … }, qui entoure les blocs de code habituel.

Transform { rotation x y z radius children [ … description d’un objet … ] }

• Regardez l’exemple suivant (rotation1.wrl) qui déplace un cône rouge à gauche et retourne un cône jaune:

  #VRML V2.0 utf8 #Description de 2 cones inverses #Description et deplacement du cone rouge Transform { translation -2 0 0 children [ Shape { geometry Cone { } appearance Appearance { material Material { diffuseColor 1 0 0 } } } ] } #Description et rotation du cone jaune Transform { rotation 1 0 0 3.1416 children [ Shape { geometry Cone { } appearance Appearance { material Material { diffuseColor 1 1 0 } } } ] }

Le terme rotation est suivi de 4 chiffres qui correspondent à: X Y Z Radius

Les valeurs de XYZ se situent entre 0 et 1 (0 = pas de rotation sur l’axe; 1 = rotation complète sur l'axe).

La valeur du radius indique la valeur de la rotation qui sera effectuée sur tout axe ayant une valeur supérieure à 0. Le radius est exprimé en radian selon la correspondance suivante avec les degrés:

30°	0.5236
60°	1.0472
90°	1.5708
180°	3.1416
270°	4.7124

Dans l'exemple précédent, la ligne:

rotation 1 0 0 3.1416

signifie que le cône subit une rotation sur l'axe des X avec un valeur de 3.1416, ce qui équivaut à une rotation en avant de 180°. Par contre, le cône ne basculera ni sur l’axe des Y, ni sur celui des Z, car leur valeur est égale à 0.

Exercice: Décrire deux cônes selon l’illustration suivante…

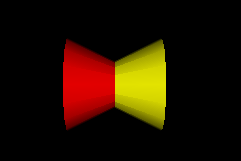
(Le cône rouge est orienté vers la droite et le jaune vers la gauche)

Solution dans le fichier rotation2.wrl

La dernière transformation que nous allons apprendre est la mise à l’échelle. Elle nous permettra d’aplatir les objets ou de les agrandir, proportionnellement ou non.

En bougeant les objets des exemples suivants, vous pourrez voir les effets de cette transformation que l’on nomme, en langage VRML, scale.

Le scale est une transformation que l’on effectue de la même manière que la translation et la rotation à l’aide d’un bloc de code Transform { … }, qui entoure les blocs de code habituel.

Transform { scale x y z children [ … description d’un objet … ] }

• Regardez en détail le code de l’exemple cylindreplat.wrl:

  #VRML V2.0 utf8 #Description d'un cylindre aplati Transform { scale 2 2 1 children [ Shape { geometry Cylinder { } appearance Appearance { material Material { diffuseColor 1 1 0 } } } ] }

On peut noter dans cet exemple, que le terme scale est suivi de 3 chiffres qui correspondent à:

X Y Z

La valeur de XYZ correspond au multiple que l’on veut appliquer à la dimension de l’objet.

Dans l’exemple ci-dessus, on étire deux fois l’objet en X, deux fois en Y, et une fois en Z (= x1, ce qui ne modifie pas l’objet par rapport à cet axe).

Nous avons vu jusqu’à maintenant les trois transformations séparément, mais il est possible de les effectuer dans le même bloc de code Transform { … }.

Les trois exemples précédents ont tous subi une rotation en même temps que la mise à l’échelle.

• Reprenons le code entier de l'exemple cylindreplat.wrl:

  #VRML V2.0 utf8 #Description d'un cylindre aplati Transform { rotation 1 0 0 1.0472 scale 2 2 1 children [ Shape { geometry Cylinder { } appearance Appearance { material Material { diffuseColor 1 1 0 } } } ] }

Les programmeurs trouvent toujours un moyen pour se simplifier la vie. Ainsi, il leur semble absurde de décrire deux fois le même objet.

Pour cette raison, il existe la possibilité de définir un objet en lui donnant une étiquette (DEF). Plus tard, on pourra rappeler cet objet à l’aide de son étiquette. C’est le principe utilisé dans le fichier scaleformes.wrl, que nous allons examiner en détail.

#VRML V2.0 utf8 #Description d'un cone DEF Cone1 Shape { geometry Cone { } appearance Appearance { material Material { diffuseColor 1 1 0 } } } Transform { translation 2 0 0 scale 0.5 2 1 children USE Cone1 }

Dans cet exemple, un premier cône jaune est décrit à l’aide d’un bloc de code Shape {…} et on lui rajoute une étiquette

DEF Cone1

• DEF est le code en VRML pour signaler que le mot qui suit est une étiquette.
• Cone1 est le nom que je décide de donner à mon premier cône. Nous pourrions l’appeler autrement…

Par la suite, dans un bloc de code Transform { … }, nous allons rappeler ce cône à l’aide de son étiquette. Ce que nous faisons sous la forme suivante:

children USE Cone1

Dans ce bloc de code Transform {…}, nous pouvons commander n’importes quelles transformations, une rotation, une translation et/ou une mise à l’échelle.

Exercice: Décrire deux cônes selon l’illustration suivante…

Les dimensions des cônes sont:
• hauteur: 2 unités
• bottomRadius: 1 unité

Solution dans le fichier 2cones.wrl

Contenu